Create an SEIR model

Create an SEIR model to be used by the simulation framework.

Usage

SEIR(u0, tspan, events = NULL, beta = NULL, epsilon = NULL, gamma = NULL)

Arguments

u0

A data.frame with the initial state in each node, i.e., the number of individuals in each compartment in each node when the simulation starts (see ‘Details’). The parameter u0 can also be an object that can be coerced to a data.frame, e.g., a named numeric vector will be coerced to a one row data.frame.

tspan

A vector (length >= 1) of increasing time points where the state of each node is to be returned. Can be either an integer or a Date vector. A Date vector is coerced to a numeric vector as days, where tspan[1] becomes the day of the year of the first year of tspan. The dates are added as names to the numeric vector.

events

a data.frame with the scheduled events, see SimInf_model.

beta

A numeric vector with the transmission rate from susceptible to infected where each node can have a different beta value. The vector must have length 1 or nrow(u0). If the vector has length 1, but the model contains more nodes, the beta value is repeated in all nodes.

epsilon

A numeric vector with the incubation rate from exposed to infected where each node can have a different epsilon value. The vector must have length 1 or nrow(u0). If the vector has length 1, but the model contains more nodes, the epsilon value is repeated in all nodes.

gamma

A numeric vector with the recovery rate from infected to recovered where each node can have a different gamma value. The vector must have length 1 or nrow(u0). If the vector has length 1, but the model contains more nodes, the beta value is repeated in all nodes.

Value

A SimInf_model of class SEIR

Details

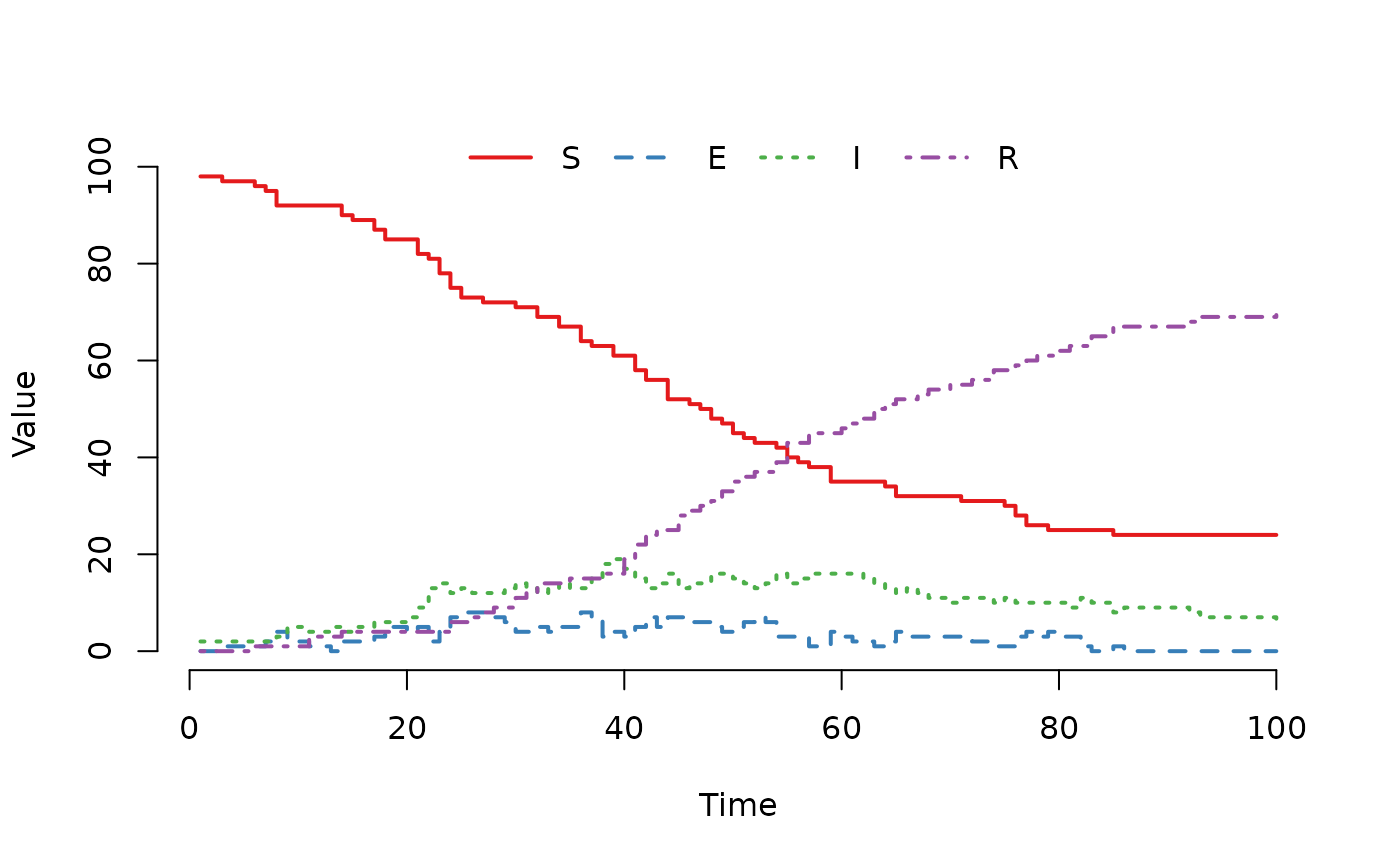
The SEIR model contains four compartments; number of susceptible (S), number of exposed (E) (those who have been infected but are not yet infectious), number of infectious (I), and number of recovered (R). Moreover, it has three state transitions,

$$S \stackrel{\beta S I / N}{\longrightarrow} E$$ $$E \stackrel{\epsilon E}{\longrightarrow} I$$ $$I \stackrel{\gamma I}{\longrightarrow} R$$

where \(\beta\) is the transmission rate, \(\epsilon\) is the incubation rate, \(\gamma\) is the recovery rate, and \(N=S+E+I+R\).

The argument u0 must be a data.frame with one row for each node with the following columns:

S

The number of sucsceptible in each node

E

The number of exposed in each node

I

The number of infected in each node

R

The number of recovered in each node

Examples

## Create a SEIR model object.
model <- SEIR(u0 = data.frame(S = 99, E = 0, I = 1, R = 0),
              tspan = 1:100,
              beta = 0.16,
              epsilon = 0.25,
              gamma = 0.077)

## Run the SEIR model and plot the result.
set.seed(3)
result <- run(model)
plot(result)